Темата на тази статия е изчисляването на поликарбонатен навес със собствените си ръце. Трябва да се научим да изчисляваме основните параметри на конструкцията, свързани с нейната здравина и размери. И така, да вървим.

Какво изчисляваме
Трябва да се научим да изчисляваме:
- Дебелината на поликарбоната и стъпката на щайгата в зависимост от очакваното натоварване от сняг на квадратен метър.
- Размери на капака на арката (което от гледна точка на геометрията се свежда до изчисляване на дължината на дъгата).
За пояснение: ние проучваме начини за изчисляване на дъгата за известни радиус и ъгъл на сектора, както и за случая, когато знаем само разстоянията между крайните точки на повърхността на дъгата.
- Минимално сечение на тръбата с известно натоварване на огъване.
В този ред ще продължим.
Дебелина на обшивката и покритието
Нека започнем с изчисляването на натоварването от сняг.
Преди да разберем как да изчислим поликарбонатен навес, ще формулираме няколко предположения, на които се основава изчислението.
- Дадените данни са от значение за висококачествен материал без признаци на разрушаване от ултравиолетово лъчение. Поликарбонатът без UV филтър става крехък след 2-3 години работа на светлина.

- Умишлено пренебрегваме ограничената деформационна стабилност на щайгата, считайки я за абсолютно здрава.
И сега - таблица, която ще ви помогне да изберете оптималната дебелина на поликарбоната и стъпката на щайгата.
| Натоварване, kg/m2 | Размери на клетката на щайгата с дебелина на поликарбоната, мм | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050x790 | 1200x900 | 1320x920 | 1250x950 |
| 900x900 | 950x950 | 1000x1000 | 1100x1100 | |
| 820x1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880x660 | 1000x750 | 1050x750 | 1150x900 |
| 760x760 | 830x830 | 830x830 | 970x970 | |
| 700x860 | 750x900 | 750x950 | 850x1050 | |
| 200 | 800x600 | 850x650 | 950x700 | 1100x850 |
| 690x690 | 760x760 | 780x780 | 880x880 | |
| 620x780 | 650x850 | 700x850 | 750x950 | |
Арх
Изчисляване по радиус и сектор
Как да изчислим арката за навес, ако знаем радиуса на огъване и сектора на дъгата?

Формулата ще изглежда като P=pi*r*n/180, където:
- P е дължината на дъгата (в нашия случай дължината на поликарбонатен лист или профилна тръба, която ще стане елемент на рамката).
- pi е числото "pi" (при изчисления, които не изискват изключително висока точност, обикновено се приема равно на 3,14).
- r е радиусът на дъгата.
- n е ъгълът на дъгата в градуси.
Нека, като пример, изчислим със собствените си ръце дължината на арката на сенника с радиус 2 метра и сектор 35 градуса.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 метра.
В процеса на работа често възниква обратната ситуация: необходимо е да се коригира радиусът и секторът на дъгата към фиксирана дължина на дъгата. Причините са ясни: цената на поликарбоната е достатъчно висока, за да минимизира количеството отпадъци.
Очевидно в този случай произведението на сектора и радиуса ще бъде равно на P/pi*180.
Нека се опитаме да поставим арката под стандартен лист с дължина 6 метра. 6/3,14*180=343,9 (със закръгляване). Освен това - прост избор на стойности с калкулатор в ръка: например за дъгов сектор от 180 градуса можете да вземете радиуса, равен на 343,9 / 180 \u003d 1,91 метра; с радиус от 2 метра секторът ще бъде равен на 343,9 / 2 \u003d 171,95 градуса.
Изчисляване по акорди
Как изглежда изчисляването на дизайна на поликарбонатен навес с арка, ако имаме информация само за разстоянието между ръбовете на арката и нейната височина?
В този случай се прилага така наречената формула на Хюйгенс. За да го използваме, нека мислено разделим хордата, свързваща краищата на арката наполовина, след което начертаваме перпендикуляр на хордата в средата.
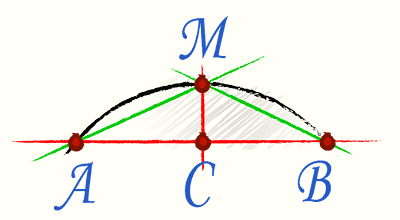
Самата формула има вида Р=2l+1/3*(2l-L), където l е хордата AM, а L е хордата AB.
Важно: изчислението дава приблизителен резултат. Максималната грешка е 0,5%; колкото по-малък е ъгловият сектор на арката, толкова по-малка е грешката.
Нека изчислим дължината на арката за случая, когато AB \u003d 2 m и AM - 1,2 m.
P=2*1.2+1/3*(2*1.2-2)=2.4+1/3*0.4=2.533 метра.
Изчисляване на сечението с известно натоварване на огъване
Доста житейска ситуация: част от сенника е козирка с известна дължина. Можем грубо да изчислим пиковото снежно натоварване върху него. Как да изберем профилна тръба с такова сечение за греди, така че да не се огъва при натоварване?

Забележка! Умишлено не засягаме как да изчислим натоварването на сенника. Оценката на натоварването от сняг и вятър е напълно самодостатъчна тема за отделна статия.
За да изчислим, имаме нужда от две формули:
- M = FL, където M е огъващият момент, F е силата, приложена към края на лоста в килограми (в нашия случай теглото на снега върху козирката), а L е дължината на лоста (дължината на гредата, която поема натоварването от снега, от ръба до точковите крепежни елементи) в сантиметри.
- M/W=R, където W е съпротивителният момент, а R е якостта на материала.
И как ще ни помогне тази купчина неизвестни стойности?
Само по себе си нищо. Някои референтни данни липсват за изчислението.
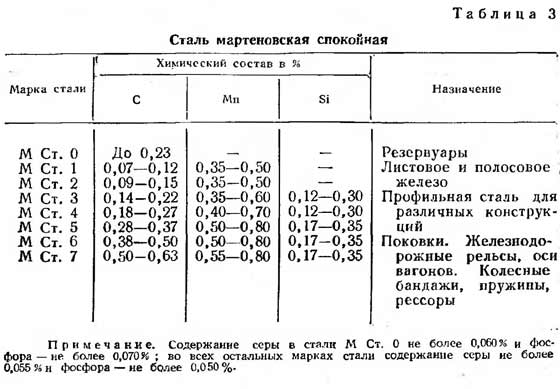
| марка стомана | Якост (R), kgf / cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Справка: Стоманите St3, St4 и St5 обикновено се използват за професионални тръби.
Сега, въз основа на данните, с които разполагаме, можем да изчислим съпротивителния момент на огъване на профилната тръба. Нека го направим.
Да предположим, че 400 килограма сняг се натрупват върху двуметров навес с три носещи греди от стомана St3.За да опростим изчисленията, ще се съгласим, че целият товар пада върху ръба на козирката. Очевидно натоварването на всяка греда ще бъде 400/3=133,3 kg; с двуметров лост моментът на огъване ще бъде равен на 133,3 * 200 \u003d 26660 kgf * cm.
Сега изчисляваме момента на съпротивление W. От уравнението 26660 kgf * cm / W = 2100 kgf / cm2 (якост на стомана) следва, че моментът на съпротивление трябва да бъде най-малко 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Как стойността на момента на съпротивление ще ни доведе до размерите на тръбата? Чрез таблиците за асортимент, съдържащи се в GOST 8639-82 и GOST 8645-68, регулиращи размерите на квадратни и фасонни тръби. За всеки размер те посочват съответния момент на съпротивление, а за правоъгълно сечение - по всяка от осите.
След проверка на таблиците установяваме, че минималният размер на квадратна тръба с необходимите характеристики е 50x50x7,0 mm; правоъгълен (с вертикална ориентация на по-голямата страна) - 70x30x5.0 mm.

Заключение
Надяваме се, че не сме преуморили читателя с изобилие от сухи цифри и формули. Както винаги, допълнителна информация за методите за изчисляване и проектиране на поликарбонатни навеси можете да намерите във видеоклипа в тази статия. Късмет!
Статията помогна ли ви?